Евклидова геометрия — геометрия и искусство

Связанные области

Если отказаться от 3-го и 4-го постулатов Евклида (т.е. терминов «круг» и «прямой угол») или, для более точного определения, ограничиться аксиомами Гильберта о связи и параллелях , получится аффинная геометрия . Впервые он был разработан Леонардом Эйлером . Термины «расстояние» и «угловая мера» здесь не используются, но есть отношения расстояния и параллелизм.

Если аксиому параллелей заменить условием, что две прямые, расположенные в одной плоскости, всегда должны иметь пересечение, аффинная геометрия становится проективной геометрией .

Если опустить аксиомы расположения и непрерывности, аффинная и проективная геометрии также могут состоять из конечного числа точек.

В синтетической геометрии понятие евклидовой плоскости обобщается таким образом, что именно те плоскости, чьи аффинные координаты лежат в евклидовом теле, являются евклидовыми плоскостями.

Линейная оболочка

Линейной оболочкой L(X) подмножества X линейного пространства V называется совокупность всевозможных линейных комбинаций элементов из X,

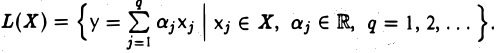
Последнее читается так: «линейная оболочка L(X) состоит из всевозможных элементов у, представимых в виде линейных комбинаций элементов множества X».

Основные свойства линейной оболочки

1. Линейная оболочка L(X) содержит само множество X.
2. L(X) — линейное подпространство пространства V.

Сумма линейных комбинаций элементов множества X и произведение линейной комбинации элементов на любое число снова являются линейными комбинациями элементов множества X.

3. L(X) — наименьшее линейное подпространство, содержащее множество X.

Это свойство следует понимать так: если линейное подпространство W содержит множество X , то W содержит и его линейную оболочку L(X).

Пусть W — линейное подпространство, содержащее заданное множество X. Тогда произвольная линейная комбинация элементов множества X — элемент линейной оболочки L(X) — содержится и в подпространстве W.

Пример:

Рассмотрим в линейном пространстве R3 две тройки ξ = (1,1,0) и η = (1,0, I) (рис.4). Множество решений уравнения

является линейной оболочкой L(ξ , η) троек ξ и η. Действительно, тройки (I, 1, 0) и (1, 0, I) образуют фундаментальную систему решений однородного уравнения (2), и значит, любое решение этого уравнения является их линейной комбинацией.

Пример:

Рассмотрим в линейном пространстве С(- ∞, ∞) вещественнозначных функций, непрерывных на всей числовой оси, набор X одночленов 1, х,…, хn:

Линейная оболочка L(X) представляет собой совокупность многочленов с вещественными коэффициентами, степени которых не превосходят n.

Обозначение:

Евклидова геометрия как теория измерения

Евклидова геометрия — это также геометрия, в которой линиям и углам назначаются размеры.

В аксиоматической структуре евклидовой геометрии числа, по- видимому, вообще не появляются. Тем не менее, указывается, как совпадающая линия добавляется к строке в том же направлении, то есть как она удваивается — и, следовательно, также умножается на любое натуральное число . Также существует конструкция для разделения заданного пути на n равных частей. Если какая-либо линия теперь помечена как единичная линия, можно построить линии, мерой которых является любое рациональное число . Это основной предмет древнегреческой арифметики .

Другие конструкции приводят к расстояниям, которые не имеют рационального числа в качестве меры. (Например, диагональ квадрата на единичном расстоянии или его участки при делении согласно золотому сечению .) Доказательство этого свидетельствует о невероятно высоком уровне греческой математики даже во времена пифагорейцев . Таким образом, введение иррациональных чисел необходимо. 2000 лет спустя аксиома полноты Гильберта гарантирует, что все действительные числа могут выступать в качестве меры расстояний.

Определение размеров для углов аналогично. Нет необходимости определять «стандартный угол », поскольку полный угол (или прямой угол ) является объективным размером. С другой стороны, разделить угол на равные части гораздо сложнее; Ни в коем случае нельзя построить угол для каждого рационального угла. Даже трехстороннее деление угла вообще не удается.
п{\ displaystyle n}

Введенная таким образом метрика эквивалентна евклидовой метрике «аналитической» или индуцированной евклидовой нормой . Для точек даны их координаты и поэтому
.
Р.2{\ Displaystyle \ mathbb {R} ^ {2}}Р.3{\ Displaystyle \ mathbb {R} ^ {3}}Иксзнак равно(Икс1,Икс2,Икс3){\ displaystyle x = (x_ {1}, x_ {2}, x_ {3})}узнак равно(у1,у2,у3){\ displaystyle y = (y_ {1}, y_ {2}, y_ {3})}d(Икс,у)знак равно(Икс1-у1)2+(Икс2-у2)2+(Икс3-у3)2{\ displaystyle d (x, y) = {\ sqrt {(x_ {1} -y_ {1}) ^ {2} + (x_ {2} -y_ {2}) ^ {2} + (x_ {3 } -y_ {3}) ^ {2}}}}

В аналитической геометрии размеры углов могут быть определены с помощью векторов.

Н. г. в виде проективных моделей[править | править код]

Через точку Р проходит бесконечно много «прямых», не пересекающих «прямой» а

Пусть на проективной плоскости введены проективные однородные координаты (x1,x2,x3)(x_1, x_2, x_3)
и задана некоторая овальная линия второго порядка, обозначаемая дальше буквой k, например

Каждое проективное отображение проективной плоскости на себя, которое оставляет на месте линию k, называется автоморфизмом относительно k. Каждый автоморфизм отображает внутренние точки линии k также во внутренние её точки. Множество всех автоморфизмов относительно линии k составляет группу. Пусть рассматриваются только точки проективной плоскости, лежащие внутри k; хорды линии k называются «прямыми». Две фигуры пусть считаются равными, если одна из них переводится в другую некоторым автоморфизмом. Так как автоморфизмы составляют группу, то имеют место основные свойства равенства фигур: если фигура А равна фигуре В, то В равна А; если фигура А равна фигуре В, а В равна фигуре С, то А. равна С. В получаемой т. о. геометрические теории будут соблюдены требования всех аксиом евклидовой геометрии, кроме аксиомы о параллельных: вместо этой последней аксиомы соблюдается аксиома о параллельных Лобачевского (см. рисунок). Тем самым получается истолкование (двумерной) геометрии Лобачевского при помощи объектов проективной плоскости или, как говорят, проективная модель геометрии Лобачевского; линию k называют абсолютом этой модели. Автоморфизмы относительно k играют роль движений. Поэтому геометрию Лобачевского можно рассматривать как теорию, изучающую свойства фигур и связанные с фигурами величины, которые остаются неизменными при автоморфизмах; короче говоря, геометрию Лобачевского можно рассматривать как теорию инвариантов группы автоморфизмов относительно овального абсолюта.

Геометрия Римана (двумерная) допускает сходное истолкование; именно она является теорией инвариантов относительно нулевого абсолюта

При этом в качестве точек и прямых модели берутся все точки и прямые проективной плоскости; автоморфизмы определяются чисто алгебраически как линейные преобразования, которые переводят уравнение (10) в уравнение того же вида.

Евклидову геометрию также можно рассматривать как теорию инвариантов некоторой группы проективных преобразований, именно, группы автоморфизмов относительно вырожденного абсолюта

то есть относительно мнимых точек (1, i, 0), (1, —i, 0); эти точки называют круговыми точками. Предметом модели являются все точки проективной плоскости, кроме точек прямой x3=x_3 = 0
, и все прямые проективной плоскости, кроме прямой x3=x_3 = 0
. В последнем случае автоморфизмы играют роль подобных преобразований, а не движений, как в случае Н. г.
Рассмотренные модели относятся к двумерным геометриям; проективные модели высших размерностей строятся аналогично.

Соответственно характеру уравнений абсолютов, геометрия Лобачевского называется гиперболической, геометрия Римана — эллиптической, геометрия Евклида — параболической.

Н. г. имеют существенные приложения в математике (теории аналитических функций, теории групп и др.) и смежных с нею областях (например, в теории относительности). Эти приложения основаны на том, что разнообразные конкретные модели Н. г. связаны с различными объектами и понятиями указанных разделов математики и смежных с нею областей.

Аксиоматика

Задача аксиоматизации элементарной геометрии состоит в построении системы аксиом так,
чтобы все утверждения евклидовой геометрии следовали из этих аксиом чисто логическим выводом без наглядности чертежей.

В «Началах» Евклида была дана следующая система аксиом:

1. От всякой точки до всякой точки можно провести прямую линию.
2. Ограниченную прямую можно непрерывно продолжать по прямой.
3. Из всякого центра всяким радиусом может быть описан круг.
4. Все прямые углы равны между собой.
5. Если прямая, пересекающая две прямые, образует внутренние односторонние углы, меньшие двух прямых углов, то, продолженные неограниченно, эти две прямые встретятся с той стороны, где углы меньше двух прямых углов.

Эта система была достаточна для того, чтобы один математик понял другого,
но в доказательствах неявно использовались и другие интуитивно очевидные утверждения, в частности так называемая теорема Паша, которая не может быть выведена из постулатов Евклида.

В 1899 году Гильберт предложил первую достаточно строгую аксиоматику евклидовой геометрии.
Попытки улучшения евклидовой аксиоматики предпринимались до Гильберта Пашем, Шуром, Пеано, Веронезе, однако подход Гильберта, при всей его консервативности в выборе понятий, оказался более успешным.

Существуют и другие современные аксиоматики, наиболее известные:

• аксиоматика Александрова;
• аксиоматика Биргофа, содержащая всего 4 аксиомы, но использующая вещественные числа как готовое понятие;
• аксиоматика Тарского.

Примеры

Наглядными примерами евклидовых пространств могут служить пространства:

• E1{\displaystyle \mathbb {E^{1}} } размерности 1{\displaystyle 1} (вещественная прямая — к примеру, числовая ось);
• E2{\displaystyle \mathbb {E^{2}} } размерности 2{\displaystyle 2} (евклидова плоскость);
• E3{\displaystyle \mathbb {E^{3}} } размерности 3{\displaystyle 3} (евклидово трёхмерное пространство).

Более абстрактный пример:

пространство Pn{\displaystyle {\mathcal {P}}^{n}} вещественных многочленов, степени которых не превосходят n, со скалярным произведением, определённым как интеграл их произведения по конечному отрезку (или по всей прямой, но с быстро спадающей весовой функцией, например e−x2{\displaystyle e^{-x^{2}}}).

Примеры геометрических фигур в многомерном евклидовом пространстве:

• правильные многомерные многогранники (например, N-мерный куб, N-мерный октаэдр, N-мерный тетраэдр);
• гиперсфера;
• .

Краткая биография

Биография Евклида до конца не изучена, к примеру, до сих пор неизвестен год рождения. Известно, что он появился на свет в небольшом районе Афин и был платоновским учеником.

Подъем его научной работы пришелся на правление Птолемея Первого. Некоторые сведения о его жизни можно проследить по арабским рукописям и архимедовым письмам к друзьям. Так, по ним можно определить, что Евклид был сыном греческого ученого и жил около Тира в Сирии.

С малых лет получал знания о мире от своего отца, он же привил сыну любовь к естественным наукам, а затем Евклид поступил в школу Платона, где и обучился математическим основам.

Повзрослев, его пригласили в храм Мусейон (по другим данным он был одним из его основателей), в котором собирались видные ученые с поэтами. Тут были классы для занятий. Также храм был заполнен садами с башнями астрономии, помещениями для одиноких размышлений и большой библиотекой.

В Мусейоне он смог открыть школу с лучшими математиками и монументальный труд в области математики, в котором заложил планиметрические основы со стереометрией, теорией чисел, законами алгебры, методами нахождения площадей с объемами и др.

Фрагмент папируса с текстом «Начал» Евклида

Монументальный труд — публикация «Начала». Это серия из 13 книг, представляющая собой обработанные публикации древнегреческих математиков с пятого по четвертый век до нашей эры.

Кроме «Начал», было создано еще одно сочинение — «Данные», в котором были опубликованы основы по геометрическому анализу. Кроме того, александрийский ученый создал учебник, с помощью которого в то время и сейчас изучают астрономию, перспективу, отражение в зеркале, музыкальные интервалы и решают тригонометрические задачи.

Все оставшиеся годы жизни посвятил изучению естественных наук и математических законов, отчего его называют отцом геометрии. О других аспектах его жизни неизвестно до сих пор. Умер в Александрии.

Это интересно: 231,ДУХОВНАЯ КУЛЬТУРА — разбираемся внимательно

Формальное определение

Чтобы дать определение евклидова пространства, в качестве основы проще всего использовать понятие скалярного произведения. Евклидово векторное пространство определяется как конечномерное векторное пространство над полем вещественных чисел, на парах векторов которого задана вещественнозначная функция (⋅,⋅),{\displaystyle (\cdot ,\cdot ),} обладающая следующими тремя свойствами:

• Билинейность: для любых векторов u,v,w{\displaystyle \mathbf {u,v,w} } и для любых вещественных чисел a,b{\displaystyle a,b} справедливы соотношения (au+bv,w)=a(u,w)+b(v,w){\displaystyle (a\mathbf {u} +b\mathbf {v} ,\mathbf {w} )=a\mathbf {(u,w)} +b\mathbf {(v,w)} } и (u,av+bw)=a(u,v)+b(u,w);{\displaystyle (\mathbf {u} ,a\mathbf {v} +b\mathbf {w} )=a\mathbf {(u,v)} +b\mathbf {(u,w)} ;}
• Симметричность: для любых векторов u,v{\displaystyle u,v} верно равенство (u,v)=(v,u);{\displaystyle \mathbf {(u,v)=(v,u)} ;}
• Положительная определённость: (u,u)⩾{\displaystyle \mathbf {(u,u)} \geqslant 0} для любого u,{\displaystyle u,} причём (u,u)=⇒u={\displaystyle \mathbf {(u,u)} =0\Rightarrow \mathbf {u} =0.}

Аффинное пространство, соответствующее такому векторному пространству, называется евклидовым аффинным пространством или просто евклидовым пространством.

Пример евклидова пространства — координатное пространство Rn,{\displaystyle \mathbb {R} ^{n},} состоящее из всевозможных наборов вещественных чисел (x1,x2,…,xn),{\displaystyle (x_{1},x_{2},\ldots ,x_{n}),} скалярное произведение где определяется формулой (x,y)=∑i=1nxiyi=x1y1+x2y2+⋯+xnyn.{\displaystyle \mathbf {(x,y)} =\sum _{i=1}^{n}x_{i}y_{i}=x_{1}y_{1}+x_{2}y_{2}+\cdots +x_{n}y_{n}.}

Длины и углы

Заданного на евклидовом пространстве скалярного произведения достаточно для того, чтобы ввести геометрические понятия длины и угла. Длина вектора u{\displaystyle u} определяется как (u,u){\displaystyle {\sqrt {\mathbf {(u,u)} }}} и обозначается |u|.{\displaystyle |\mathbf {u} |.} Положительная определённость скалярного произведения гарантирует, что длина ненулевого вектора ненулевая, а из билинейности следует, что |au|=|a||u|,{\displaystyle |a\mathbf {u} |=|a||\mathbf {u} |,} то есть длины пропорциональных векторов пропорциональны.

Угол между векторами x{\displaystyle \mathbf {x} } и y{\displaystyle \mathbf {y} } определяется как arccos⁡(x,y)|x||y|.{\displaystyle \arccos \mathbf {\tfrac {(x,y)}{|x||y|}} .} Из теоремы косинусов следует, что для двумерного евклидова пространства (евклидовой плоскости) данное определение угла совпадает с обычным. Ненулевыеортогональные векторы, как и в трёхмерном пространстве, можно определить как векторы под углом π2,{\displaystyle {\tfrac {\pi }{2}},} то есть как векторы с нулевым скалярным произведением.

Замечание

Необходимо уточнить, что, чтобы арккосинус от (x,y)|x||y|{\displaystyle \mathbf {\tfrac {(x,y)}{|x||y|}} } был определён, необходимо и достаточно, чтобы выполнялось неравенство |(x,y)|x||y||⩽1.{\displaystyle \left|\mathbf {\tfrac {(x,y)}{|x||y|}} \right|\leqslant 1.} Это неравенство действительно выполняется в произвольном евклидовом пространстве: оно называется неравенством Коши — Буняковского. Из него, в свою очередь, следует неравенство треугольника: |u+v|⩽|u|+|v|.{\displaystyle \mathbf {|u+v|\leqslant |u|+|v|} .} Неравенство треугольника, вместе с вышеперечисленными свойствами длины, означает, что длина вектора является нормой на евклидовом векторном пространстве, а функция d(x,y),{\displaystyle d\mathbf {(x,y)} ,} или |x−y|,{\displaystyle \mathbf {|x-y|} ,} задаёт на евклидовом пространстве структуру метрического пространства (эта функция называется евклидовой метрикой). В частности, расстояние между элементами (точками) x{\displaystyle \mathbf {x} } и y{\displaystyle \mathbf {y} } координатного пространства Rn{\displaystyle \mathbb {R} ^{n}} задаётся формулой d(x,y)=‖x−y‖=∑i=1n(xi−yi)2.{\displaystyle d(\mathbf {x} ,\mathbf {y} )=\|\mathbf {x} -\mathbf {y} \|={\sqrt {\sum _{i=1}^{n}(x_{i}-y_{i})^{2}}}.}

биография

Нет прямого источника о жизни Евклида: у нас нет ни письма, ни автобиографических указаний (даже в виде предисловия к произведению), ни официальных документов, ни даже намеков кого-либо из его современников. Как резюмирует историк математики Питер Шрайбер, «о жизни Евклида не известно ни одного достоверного факта».

Написание старейшего известно о жизни появляется Евклид в сводке по истории геометрии , написанного V — го  века нашей эры философа неоплатоник Прокл , комментатор первой книги элементов . Сам Прокл не дает никаких указаний. Он только говорит, что «объединив свои Элементы , скоординировал многие из них и вызвал в неопровержимых демонстрациях те, которые его предшественники демонстрировали в небрежной манере. Этот человек также жил при первом Птолемее, потому что Архимед упоминает Евклида. Таким образом, Евклид старше учеников Платона , но старше Архимеда и Эратосфена  »

Принимая во внимание временную шкалу, данную Проклом, Евклид, Платон и Архимед, жившие между современниками Птолемея I er , следовательно, жили около 300 г. до н

Ж.-К.

Ни один документ не противоречит этим нескольким предложениям или не подтверждает их. Прямое упоминание Евклида в произведениях Архимеда происходит из отрывка, который считается сомнительным. Архимед также обратиться к некоторым результатам Стихии и ostrakon , найденный на острове Элефантина и датированных III — го  века до н.э., обсуждает цифры изученные в тринадцатой книге элементов , а десятиугольника и икосаэдра , но не воспроизводят евклидовы произнесение точно; поэтому они могли происходить из источников до Евклида. Ориентировочная дата 300 г. до н.э. Однако считается, что AD совместим с анализом содержания евклидовой работы и принят историками математики.

Кроме того, намек математиком IV — го  века нашей эры, Папп Александрийский , свидетельствует о том , что ученики Евклида преподавал в Александрии . На этом основании некоторые авторы связывают Евклида с Мусионом Александрийским , но, опять же, он не упоминается ни в одном соответствующем официальном документе. Квалификатор, часто связанный с Евклидом в древности, — это просто stoichéiôtês (на древнегреческом  : στοιχειωτής ), то есть «автор Элементов».

Портрет Евклида работы Жюста де Гана, написанный около 1474 года; геодезист ошибочно отождествлен с Евклидом из Мегары из- за распространенной в то время путаницы между последним и автором .

Про Евклида ходят несколько анекдотов, но, поскольку они появляются и для других математиков, они не считаются реалистичными: это, таким образом, один из знаменитых анекдотов Прокла, согласно которому Евклид ответил бы Птолемею — который хотел более легкого пути, чем элементы  — что там не было ни царская дорога в геометрии; вариант того же анекдота на самом деле приписывают Менехму и Александру Великому . Точно так же, начиная с поздней античности , различные подробности были добавлены к рассказам о жизни Евклида без новых источников и часто противоречивым образом. Таким образом, некоторые авторы рождают Евклида в Тире , другие — в Геле , ему приписывают различные генеалогии , конкретных мастеров, разные даты рождения и смерти, независимо от того, соблюдают ли правила жанра или одобряют определенные интерпретации. Таким образом, в средние века и в начале Возрождения математика Евклида часто путали с современным философом Платона Евклидом Мегарским .

Столкнувшись с этими противоречиями и отсутствием надежных источников, историк математики Жан Итар даже предположил в 1961 году, что Евклид как личность, возможно, не существовал, и что это имя могло обозначать «собирательное название« математической школы », либо настоящий мастер в окружении учеников или даже чисто вымышленное имя. Но эта гипотеза, похоже, не принимается.

Один из самых старых дошедших до нас фрагментов Элементов Евклида, обнаруженный в Оксиринхе , датируется периодом между 75 и 125 годами до нашей эры. Мы не более чем на один процент текста Евклида в более ранних источниках в конце IX — го  века.

характеристики

Далее предполагается общий случай вещественных или комплексных векторов конечной размерности с или . Следующие свойства являются лишь частными случаями соответствующих свойств общих норм, индуцированных скалярным произведением .
v∈Kп{\ displaystyle v \ in {\ mathbb {K}} ^ {n}}Kзнак равноР.{\ Displaystyle {\ mathbb {K}} = \ mathbb {R}}Kзнак равноС.{\ Displaystyle {\ mathbb {K}} = \ mathbb {C}}

Аксиомы нормы

Векторы в неравенстве треугольника

Евклидова норма удовлетворяет трем . определённость

‖v‖2знак равно⇒vзнак равно{\ Displaystyle \ | v \ | _ {2} = 0 \; \ Rightarrow \; v = 0}

означает, что если длина вектора равна нулю , это должен быть нулевой вектор . Абсолютная однородностьv∈Kп{\ displaystyle v \ in {\ mathbb {K}} ^ {n}}

‖α⋅v‖2знак равно|α|⋅‖v‖2{\ Displaystyle \ | \ альфа \ CDOT v \ | _ {2} = | \ альфа | \ CDOT \ | v \ | _ {2}}

утверждает, что, когда компоненты вектора умножаются на число , длина вектора изменяется с величиной этого числа. Неравенство треугольника ( )
α∈K{\ displaystyle \ alpha \ in \ mathbb {K}}

‖v+ш‖2≤‖v‖2+‖ш‖2{\ Displaystyle \ | v + вес \ | _ {2} \ leq \ | v \ | _ {2} + \ | ш \ | _ {2}}

наконец, заявляет, что длина суммы двух векторов не больше суммы двух длин. Равенство применяется именно тогда, когда два вектора указывают в одном направлении. Доказательство неравенства треугольника основано на неравенстве Коши-Шварцаv,ш∈Kп{\ displaystyle v, w \ in {\ mathbb {K}} ^ {n}}

|⟨v,ш⟩|≤‖v‖2⋅‖ш‖2{\ displaystyle \ left | \ langle v, w \ rangle \ right | \ leq \ | v \ | _ {2} \ cdot \ | w \ | _ {2}}.

Сфера единства и сфера единства

Единичная сфера (синий) и открытая единичная сфера (красный) в двух измерениях

Евклидова норма является специальной р -норма для выбора и, следовательно , также называется 2-нормой. Единичная сфера евклидовой нормы, то есть множество
пзнак равно2{\ displaystyle p = 2}

{v∈Kп‖v‖2знак равно1}{\ Displaystyle \ {v \ in {\ mathbb {K}} ^ {n} \ двоеточие \ | v \ | _ {2} = 1 \}}

Векторы со стандартным топливом имеют два реальных измерения в форме круга , в трех реальных измерениях форму сферической поверхности и в общих размерах форму шара . Аналогично этому называют сумму

{v∈Kп‖v‖2≤1}{\ displaystyle \ {v \ in {\ mathbb {K}} ^ {n} \ двоеточие \ | v \ | _ {2} \ leq 1 \}} или же. {v∈Kп‖v‖2<1}{\ Displaystyle \ {v \ in {\ mathbb {K}} ^ {n} \ двоеточие \ | v \ | _ {2} <1 \}}

замкнутая или открытая единичная сфера евклидовой нормы. Он имеет форму круглого диска в двух реальных измерениях и форму сферы в трех и более измерениях . Евклидова норма также может быть определена как функционал Минковского, используя его единичную сферу .

Уравнение параллелограмма

→ Основная статья : уравнение параллелограмма

Векторы в уравнении параллелограмма

Евклидова норма достаточна для всех векторов в параллелограмм уравненияv,ш∈Kп{\ displaystyle v, w \ in {\ mathbb {K}} ^ {n}}

‖v+ш‖22+‖v-ш‖22знак равно2(‖v‖22+‖ш‖22){\ Displaystyle \ | v + вес \ | _ {2} ^ {2} + \ | vw \ | _ {2} ^ {2} = 2 (\ | v \ | _ {2} ^ {2} + \ | ш \ | _ {2} ^ {2})}

и является единственной p -нормой с этим свойством, см. также теорему Жордана-фон Неймана .

Унитарная инвариантность

Евклидова норма — также как единственная p- норма — инвариантна относительно унитарных преобразований . Поэтому, если унитарная матрица (в комплексном случае) или ортогональная матрица (в реальном случае) , то применяется
U∈Kп×п{\ Displaystyle U \ in {\ mathbb {K}} ^ {п \ раз п}}

‖Uv‖2знак равно‖v‖2{\ Displaystyle \ | УФ \ | _ {2} = \ | v \ | _ {2}},

как насчет произведения

‖Uv‖22знак равно⟨Uv,Uv⟩знак равно⟨v,UЧАСUv⟩знак равно⟨v,U-1Uv⟩знак равно⟨v,v⟩знак равно‖v‖22{\ Displaystyle \ | Uv \ | _ {2} ^ {2} = \ langle Uv, Uv \ rangle = \ langle v, U ^ {H} Uv \ rangle = \ langle v, U ^ {- 1} Uv \ rangle = \ langle v, v \ rangle = \ | v \ | _ {2} ^ {2}}

следует. Евклидова норма не меняется при унитарных преобразованиях. Для вещественных векторов такими преобразованиями являются, например, вращения вектора вокруг нулевой точки . Это свойство проявляется, например, при численном решении линейных задач наименьших квадратов с использованием метода наименьших квадратов для QR-разложений .