233,евклид

Геометрию изобрели в Древнем Вавилоне

Многие поколения людей последних нескольких сотен лет твердо убеждены, что геометрию изобрели в Древней Греции, а имя Евклида тесно связано с этой наукой. Евклид родоначальник геометрии?

Но если внимательно изучать древнюю историю, то мы можем обратить внимание, что элементарную геометрию неплохо знали и использовали древние Египтяне: им нужно было уметь правильно делить земные участки на плодородных участках в дельте Нила,  так же им нужно было строить пирамиды и здания. Однако в последнее время появились новые факты, в которых небезосновательно доказывается, что геометрия зародилась в Вавилоне

Почему в Вавилоне и почему так давно — в 35–50 годах до н.э. ?

Однако в последнее время появились новые факты, в которых небезосновательно доказывается, что геометрия зародилась в Вавилоне. Почему в Вавилоне и почему так давно — в 35–50 годах до н.э. ?

Науке давно известно, что вавилоняне обладали серьезными лля их времени достижениями в астрономии:  древнее население Южной Месопотамии могло предсказывать затмения, вычислять расстояния между звездами и планетами, собирать точные данные о видимых невооруженным глазом небесных телах. Они для определения положения Юпитера на небосводе, которому поклонялись как самому главному (верховному) божеству, называя его Мардуком, вавилоняне проводили сложные геометрические вычисления, которые, как считалось ранее, появились лишь в XIV веке в Европе. Вавилоняне обогнали свое время, а с ними достижения в геометрических знаниях древних египтян и греков!

Проблемой развития науки, в частности астрономии и геометрии в Месопотамии, в течении долгих 14 лет занимался пециалист в археоастрономии Мэтью Оссендриджвер (Mathieu Ossendrijver) из Берлинского университета имени Гумбольдта. Каждый год в течение этого времени он  ездил в Британский музей, где изучал глиняные таблички древних вавилонян (как известно, вавилоняне писали на глиняных табличках клинописными значками), где все таки разгадал загадку, которую хранили две таблички. На этих глиняных «скрижалях», как выяснилось в результате их расшифровки, были изложены инструкции для построения трапециевидной фигуры!

«Глиняные таблички показали, что вавилоняне могли вычислять движение планет в очень современном стиле — они рассчитывали зависимость скорости от времени, как это делается в современных графиках», — рассказал корреспонденту отдела науки «Газеты.Ru» автор исследования. — «Любой современный математик или физик скажет вам, что с помощью таких измерений вы сможете вычислить расстояние, которое прошло тело. Раньше считалось, что это поняли в 1350 году в Оксфорде и в Париже, но на самом деле это сделали вавилоняне в 35–50 годах до н.э. Кроме того, на табличках использованы геометрические вычисления, которые появились еще раньше — в 1800–1600 годах до н.э. Так «старая геометрия» была применена к новой ситуации».

Ученый так же отметил, что вавилонская геометрия была особенной и она отличалась своими от геометрии древних греков более абстрактными и глубокими представлениями о геометрических объектах. Такими достижениями в области абстрагирования геометры Европы смогли похвастаться только на рубеже XIV нашей эры.

Сейчас становится понятным, что все астрономические вычисления вавилонян были преданы забвению, а европейские ученые  лишь в конце Средних веков повторно изобрели то, что разработало древнее население Южной Месопотамии. По мнению автора исследования, полученные им результаты могут свидетельствовать о том, что если бы вавилонская геометрия была перенята другими народами, то в Средние века математикам не пришлось изобретать колесо. Увы, история не признает сослагательные наклонения…

Краткая биография

Биография Евклида до конца не изучена, к примеру, до сих пор неизвестен год рождения. Известно, что он появился на свет в небольшом районе Афин и был платоновским учеником.

Подъем его научной работы пришелся на правление Птолемея Первого. Некоторые сведения о его жизни можно проследить по арабским рукописям и архимедовым письмам к друзьям. Так, по ним можно определить, что Евклид был сыном греческого ученого и жил около Тира в Сирии.

С малых лет получал знания о мире от своего отца, он же привил сыну любовь к естественным наукам, а затем Евклид поступил в школу Платона, где и обучился математическим основам.

Повзрослев, его пригласили в храм Мусейон (по другим данным он был одним из его основателей), в котором собирались видные ученые с поэтами. Тут были классы для занятий. Также храм был заполнен садами с башнями астрономии, помещениями для одиноких размышлений и большой библиотекой.

В Мусейоне он смог открыть школу с лучшими математиками и монументальный труд в области математики, в котором заложил планиметрические основы со стереометрией, теорией чисел, законами алгебры, методами нахождения площадей с объемами и др.

Фрагмент папируса с текстом «Начал» Евклида

Монументальный труд — публикация «Начала». Это серия из 13 книг, представляющая собой обработанные публикации древнегреческих математиков с пятого по четвертый век до нашей эры.

Кроме «Начал», было создано еще одно сочинение — «Данные», в котором были опубликованы основы по геометрическому анализу. Кроме того, александрийский ученый создал учебник, с помощью которого в то время и сейчас изучают астрономию, перспективу, отражение в зеркале, музыкальные интервалы и решают тригонометрические задачи.

Все оставшиеся годы жизни посвятил изучению естественных наук и математических законов, отчего его называют отцом геометрии. О других аспектах его жизни неизвестно до сих пор. Умер в Александрии.

Это интересно: 231,ДУХОВНАЯ КУЛЬТУРА — разбираемся внимательно

Средневековье и Возрождение

Сохранение древних произведений и латинские переводы греческих или арабских произведений являются основным вкладом западного средневековья в геометрию.

В целом средневековье в Западной Европе для геометрии, как и для многих других наук, было периодом упадка.

Геометрию, конечно, все еще преподают. Это часть квадривиума, который также включает арифметику , астрономию и музыку . Однако квадривиум гораздо менее популярен, чем тривиум ( грамматика , риторика и диалектика ): последний, вероятно, лучше подходит для общества, основным проектом которого является подготовка к пост-земной жизни.

В течение длительного периода , который тянется примерно с V — го  века XV — го  века ученые геодезистов редкость на Западе. Мы можем упомянуть Гербера д’Орийака, который стал папой под именем Сильвестра II, и особенно Леонардо Пизанского, известного как Фибоначчи; они по-прежнему более известны своей арифметической работой и страстью, с которой они переводили работы арабских ученых …

Возрождение к XV — го  века и XVI — го  века увидел первый тремор геометрической новости с появлением конической точки зрения которого теория подвергается нападению ряда ученых, в основном итальянцы, и самый известный, вероятно , Piero Франческа , Леонардо да Винчи , и Лука Пачоли , первые двое были обязаны своей славой больше своему художественному гению, чем математике.

Из истории геометрии

Подробности

Категория: Геометрия

Документальные учебные фильмы. Серия «Геометрия».

https://vk.com/video_ext.php

 Уже первобытные люди на самой начальной ступени своего развития должны были различать формы окружавших их предметов и замечать места их расположения. Так, они запоминали места охоты, места стоянок и селений. Они постепенно научились определять расстояния между отдельными предметами, размеры отдельных участков местности и т. п. По мере развития общественной жизни людей изучение форм и размеров предметов и их взаимного расположения становилось всё более нужным и требовало от человека всё больших знаний. В древнем Египте весенние разливы огромной реки Нила смывали границы между отдельными земельными участками. Нужно было ежегодно их восстанавливать, что было связано с большими измерительными работами на местности. Чтобы выполнять эти работы, надо было иметь удобные правила для вычисления длин линий, площадей, участков земли, для выполнения планировок местности и т. п. Эти правила были выработаны и записаны. Греки, ведя торговлю с египтянами, познакомились с этими правилами, дополнили их и постепенно развили из них целую науку, которую и назвали геометрией, что значит искусство измерять землю ( — земля, — измерять). Греческий учёный Евклид, живший в III в. до н. э., особенно подробно разработал эту науку и изложил её вместе с арифметикой в одиннадцати книгах, которые он назвал «Начала». По ним и изучали геометрию в последующие века. По образцу этих «Начал» составляются учебники геометрии и до нашего времени.Наблюдая окружающие нас предметы, мы замечаем большое разнообразие их внешнего вида и их свойств. Предметы отличаются один от другого своим видом, весом, свойствами вещества, из которого они состоят, и т. д. Но при всём этом разнообразии можно заметить свойство, присущее всем предметам без исключения, именно: каждый предмет имеет свою форму и свой размер. При изготовлении различных предметов им придают форму и размер, соответствующие их назначению. Артиллерийскому снаряду придают форму, при которой он имеет нужную дальность полёта, кузову корабля—форму, которая даёт ему устойчивое положение на поверхности воды и позволяет легче рассекать волны морской стихии. Далее, мы замечаем, что каждый предмет занимает определённое положение среди других предметов

В практической жизни весьма важно уметь определять расстояние между предметами, размещать их должным образом на нужных расстояниях. Так

на заводах весьма важно правильно расставить станки. На поле боя важно правильно разместить дзоты и наблюдательные пункты, уметь определить местонахождение огневых точек врага, расстояние до его блиндажей и т. п. Изучение форм и размеров предметов и их взаимного положения составляет отдельную область человеческого знания. Наука, изучающая формы, размеры и взаимное расположение предметов, называется геометрией.

 Геометрия, как и многие другие разделы математики, своими корнями уходит в «далекое прошлое. Слово «геометрия» в переводе с греческого означает «землемерие». ‘Такое название объясняется тем, что зарождение этого раздела математики было связано с различными измерительными работами, которые приходилась выполнять при разметке земельных участков, проведении дорог, строительстве зданий и других сооружений. В результате этой деятельности появились и постепенно накапливались различные правила, связанные с геометрическими измерениями и построениями. Таким образом, геометрия возникла на основе практической деятельности людей и в начале своего развития служила в основном практическим целям. В дальнейшем геометрия сформировалась как самостоятельная наука, занимающаяся изучением геометрических фигур. Примеры геометрических фигур: треугольник, квадрат, окружность.

 Геометрические фигуры бывают весьма разнообразны. Часть любой геометрической фигуры является геометрической фигурой. Объединение нескольких геометрических фигур есть снова геометрическая фигура. На рисунке фигура слева состоит из треугольника и трех квадратов, а фигура справа состоит из окружности и частей окружности. Всякую геометрическую фигуру мы представляем себе составленной из точек.

Геометрия широко применяется на практике. Ее надо знать и рабочему, и инженеру, и архитектору, и художнику. Одним словом, геометрию надо знать всем.

Эпонимы

Следующие математические структуры названы в честь Евклида:

• Евклидово расстояние , длина прямой связи между двумя точками на плоскости или в пространстве.
• Евклидов алгоритм , метод вычисления наибольшего общего делителя двух натуральных чисел
• Евклидова геометрия , начертательная геометрия плоскости или пространства
• Евклидово твердое тело , упорядоченное твердое тело, в котором каждый неотрицательный элемент имеет квадратный корень
• Евклидова норма , длина вектора на плоскости или в пространстве
• Евклидово пространство , пространство интуиции, реальное аффинное пространство со стандартным скалярным произведением
• Евклидово отношение , отношение, к которому применимо следующее: если два элемента связаны каждый с третьим, то они также связаны друг с другом.
• Евклидово кольцо , кольцо, в котором возможно деление на остаток
• Евклидовы инструменты , допустимые действия при построении с циркулем и линейкой

Кроме того, в честь Евклида названы следующие математические теоремы и доказательства:

• Евклидово доказательство иррациональности корня из 2 , первое доказательство противоречия в истории математики
• Теорема Евклида о высоте : в прямоугольном треугольнике квадрат над высотой равен по площади прямоугольнику из сечений гипотенузы.
• Теорема Евклида о катетерах : в прямоугольном треугольнике квадраты катета равны произведению гипотенузы и соответствующего сечения гипотенузы.
• Лемма Евклида : если простое число делит произведение двух чисел, то также хотя бы один из двух множителей
• Теорема Евклида : простых чисел бесконечно много

Также назван в честь Евклида:

• Евклид (лунный кратер) , кратер на передней части Луны
• (4354) Евклид , астероид главного пояса

Необычные свойства

Четырехугольник Ламберта в гиперболической геометрии

Четырехугольники Саккери в трех геометриях

Евклидова и неевклидова геометрии, естественно, обладают многими схожими свойствами, а именно теми, которые не зависят от природы параллелизма. Эта общность является предметом абсолютной геометрии (также называемой нейтральной геометрией )

Однако исторически наибольшее внимание уделялось свойствам, которые отличают одну геометрию от других.

Помимо поведения линий относительно общего перпендикуляра, упомянутого во введении, мы также имеем следующее:

• Ламберт четырехугольник является четырехугольник с тремя прямыми углами. Четвертый угол четырехугольника Ламберта острый, если геометрия гиперболическая, прямой угол, если геометрия евклидова, или тупой, если геометрия эллиптическая. Следовательно, прямоугольники существуют (утверждение, эквивалентное постулату параллельности) только в евклидовой геометрии.
• Саккрайте четырехугольник является четырехугольник с двух сторон равной длиной, и перпендикулярно к стороне называется база . Два других угла четырехугольника Саккери называются верхними углами, и они имеют одинаковую меру. Вершины четырехугольника Саккери острые, если геометрия гиперболическая, прямые углы, если геометрия евклидова, и тупые углы, если геометрия эллиптическая.
• Сумма углов любого треугольника меньше 180 °, если геометрия гиперболическая, равна 180 °, если геометрия евклидова, и больше 180 °, если геометрия эллиптическая. Дефект треугольника это числовое значение (180 ° — сумма мер углов треугольника). Этот результат можно также сформулировать так: дефект треугольников в гиперболической геометрии положительный, дефект треугольников в евклидовой геометрии равен нулю, а дефект треугольников в эллиптической геометрии отрицателен.

Начертательная геометрия

Инженерное образование в обязательном порядке предполагает изучение начертательной геометрии наряду с другими важными дисциплинами.

Для отображения геометрических характеристик зданий, машин, механизмов создаются чертежи их конструкций, определяющие особенности формы и размеров будущего изделия.

Начертательная геометрия представляет собой теоретическую базу, без использования которой невозможно создание специальной документации, называемой техническими чертежами. Чертежи являются необходимым средством для визуального отображения идеи создания той или иной технической продукции. На чертежах, в графической форме доступной для понимания, определены точные размеры и конструкция будущего продукта, представлены методы исполнения и возможность исследования изделия и его составных частей.

Для правильного выражения своих мыслей и идей с помощью эскизов и чертежей, необходимо тщательное изучение начертательной геометрии, включающей в себя геометрические законы построения изображений различных объектов с учетом многообразия их свойств и пространственного расположения относительно друг друга.

Начертательная геометрия, являющаяся графическим средством отображения информации, нашла широкое применение в жизни человечества.

Геометрическим формам присущи образность, символичность, компактность, доступность понимания. Простота и лаконичность графических изображений способствуют их повсеместному применению во всех областях созидательной деятельности человека.

Графика используется в качестве международного языка при общении народов различной культуры и национальных особенностей. Знание графического языка является преимущественным показателем при поиске работы, способствует совершенствованию образования и расширяет возможности воплощения идей человека в жизнь.

Базовые геометрические объекты

Базовые геометрические фигуры — это точки, отрезки, лучи, прямые, плоскости.

Точка — это идеальный математический объект, у которого нет длины и ширины.

Отрезок — это часть прямой, у которого есть начало и конец.

Смежные отрезки — это отрезки, которые не лежат на одной прямой и имеют один общий конец. На рисунке изобразили смежные отрезки АВ и АС, где точка А — общий конец.

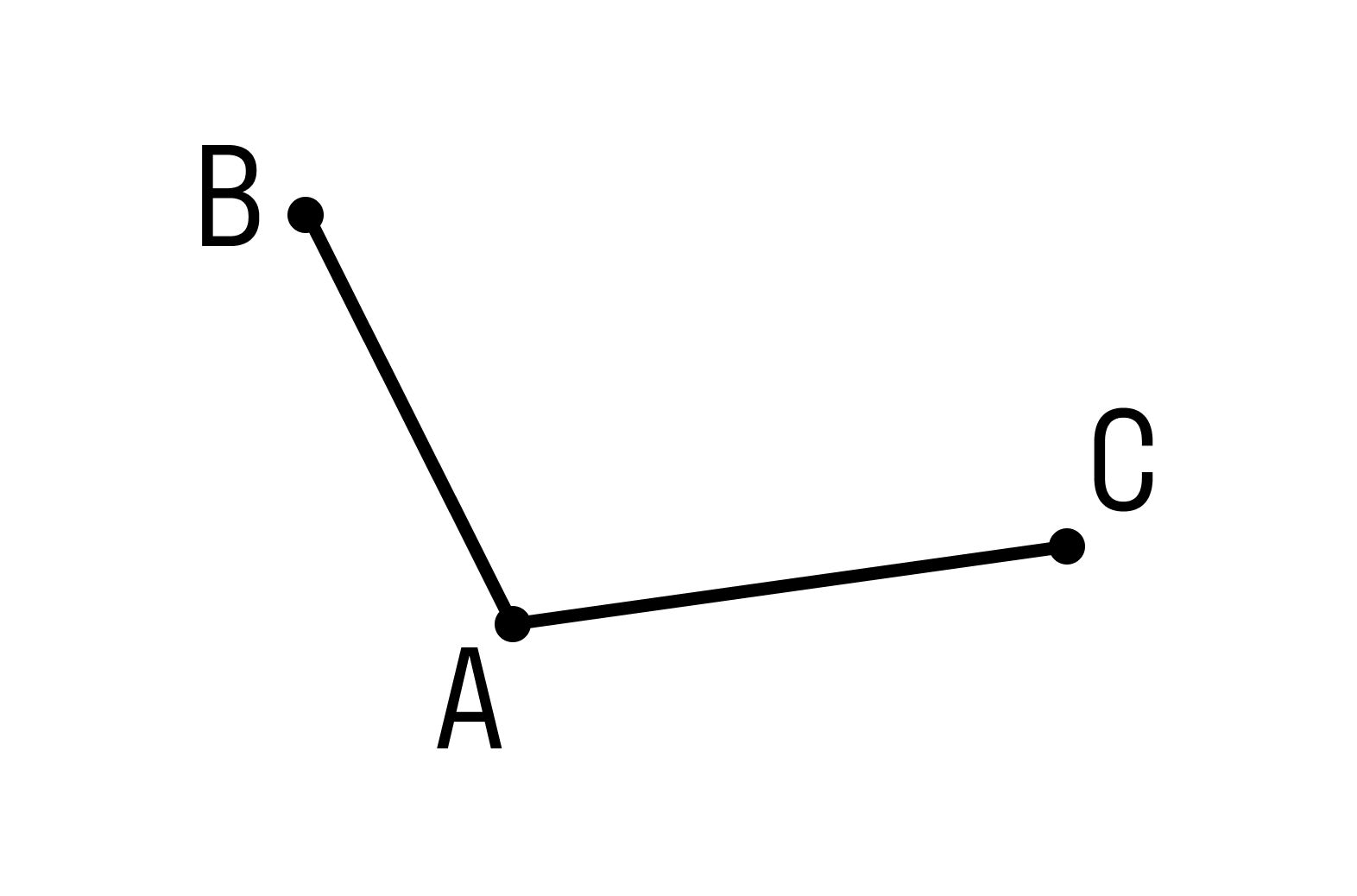
Прямая — это «не кривая». Более точное определение вряд ли можно сформулировать.

Когда мы рисуем прямую на листе бумаги, мы изображаем только ее часть, потому что прямая не имеет начала и конца.

Обозначать прямые принято малыми латинскими буквами (a, b,c), но можно и большими латинскими буквами (АВ, CD, MN). Точки всегда обозначают большими латинскими буквами (А, В, С).

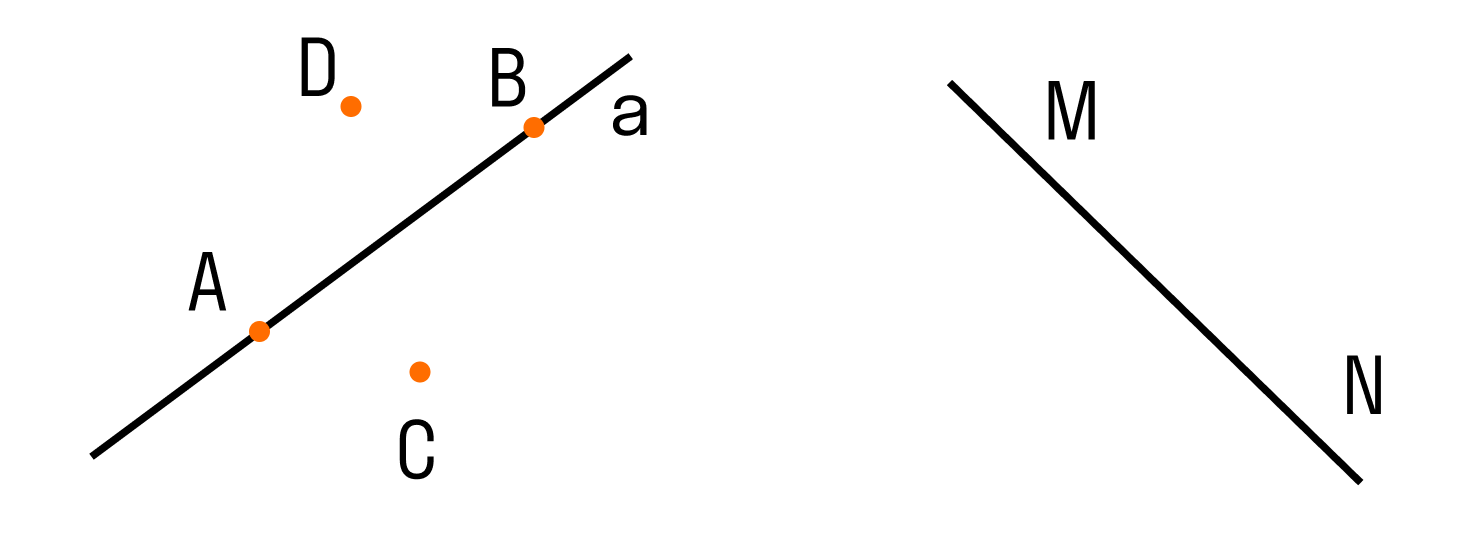
Два варианта расположения точек относительно прямой:

1. Точки лежат на данной прямой. Или еще говорят, что прямая проходит через эти точки — на рисунке выше такими точками являются А и В. При решении задач для краткости используют запись A ∈ a (читается так: точка А принадлежит прямой a или точка А лежит на прямой a), аналогично будет и для точки В (B ∈ b).
2. Точки не лежат на данной прямой. Говорят так: прямая не проходит через эти точки — на рисунке такими точками являются С и D. При решении задач для краткости используют запись C ∉ a (читается так: точка С не принадлежит прямой a или точка С не лежит на прямой a), аналогично будет и для точки D (D ∉ a).

Важно знать

Через любые две точки можно провести прямую и притом только одну.

Если рассмотреть две прямые, то возможны два варианта их расположения:

1. Прямые пересекаются, то есть имеют одну общую точку.
   Для записи пересекающихся прямых используют специальный знак — ∩ , то есть a ∩ b (читают: прямая a пересекает прямую b).
2. Прямые не пересекаются, то есть не имеют общих точек.
   Для записи не пересекающихся прямых используют специальный знак — ,
   то есть m n (читают: прямая m не пересекает прямую n).

Луч — это часть прямой, ограниченная с одной стороны. Луч имеет начало, но не имеет конца.

На рисунке точка О разбивает прямую АВ на две части:

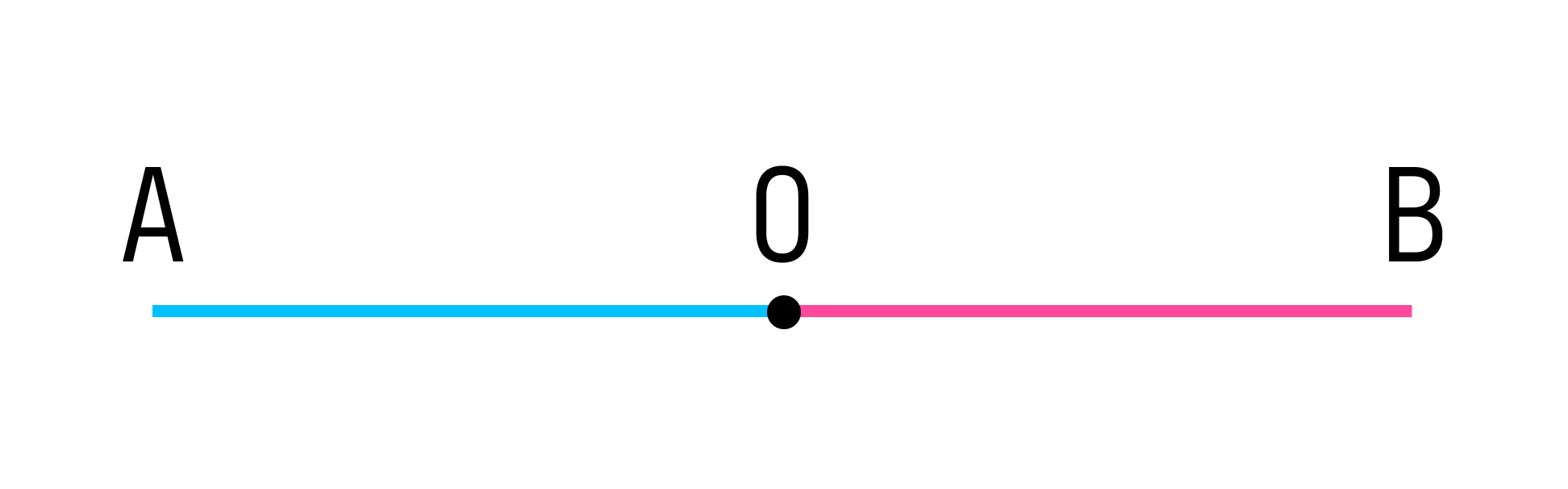
Каждая из этих частей называется лучом, а точка О является началом одного и другого луча.

Назовем получившиеся лучи:

• Луч ОА, точка О — начало луча ОА; конца у луча ОА нет.
• Луч ОВ, точка О — начало луча ОВ; конца у луча ОВ нет.

Лучи ОА и ОВ принадлежат одной прямой АВ. Лучи ОА и ОВ имеют общее начало (точка О). Лучи ОА и ОВ противоположно направлены. При таких условиях лучи ОА и ОВ называются дополнительными.

Плоскость — это бесконечная поверхность, к которой принадлежат все прямые, которые проходят через какие-либо две точки плоскости

Пифагорова тройка

Пифагорова тройка из трёх натуральных чисел (x,y,z)удовлетворяет соотношению Пифагора: x2+y2=z2. При этом числа, образующие пифагорову тройку, называются пифагоровыми числами. Треугольник, длины сторон которого равны пифагоровым числам, является прямоугольным. Простейший из них — египетский треугольник со сторонами 3,4,5: 32+42=52.

Некоторые пифагоровы тройки : (3, 4, 5), (6, 8, 10), (5, 12, 13), (9, 12, 15), (8, 15, 17), (12, 16, 20), (15, 20, 25), (7, 24, 25), (10, 24, 26), (20, 21, 29), (18, 24, 30), (16, 30, 34),(21, 28, 35), (12, 35, 37), (15, 36, 39), (24, 32, 40), (9, 40, 41), (27, 36, 45), (14, 48, 50), (30, 40, 50), …Пифагоровы тройки известны очень давно. В архитектуре древнемесопотамских надгробий встречается равнобедренный треугольник, составленный из двух прямоугольных со сторонами 9, 12 и 15 локтей. Пирамиды фараона Снофру (XXVII век до н. э.) построены с использованием треугольников со сторонами 20, 21 и 29, а также 18, 24 и 30 десятков египетских локтей.

Кинематическая геометрия

Гиперболическая геометрия нашла применение в кинематике с помощью физической космологии, введенной Германом Минковским в 1908 году. Минковский ввел такие термины, как мировая линия и собственное время, в математическую физику . Он понял, что подмногообразие событий в один момент собственного времени в будущем можно рассматривать как гиперболическое пространство трех измерений. Уже в 1890-х годах Александр Макфарлейн рисовал это подмногообразие с помощью своей « и гиперболических кватернионов , хотя Макфарлейн не использовал космологический язык, как Минковский в 1908 году. Соответствующая структура теперь называется гиперболоидной моделью гиперболической геометрии.

Неевклидовы плоские алгебры поддерживают кинематическую геометрию на плоскости. Например, разделенное комплексное число z = e a j может представлять пространственно-временное событие в один момент в будущем в системе отсчета с быстротой a . Кроме того, умножение на z равносильно преобразованию лоренцевского буста кадра с нулевой скоростью в кадр с быстротой а .

Кинематическое исследование использует двойственные числа для представления классического описания движения в абсолютном времени и пространстве : уравнения эквивалентны отображению сдвига в линейной алгебре:
zзнак равноИкс+уϵ,ϵ2знак равно,{\ displaystyle z = x + y \ epsilon, \ quad \ epsilon ^ {2} = 0,}Икс′знак равноИкс+vт,т′знак равнот{\ displaystyle x ^ {\ prime} = x + vt, \ quad t ^ {\ prime} = t}

(Икс′т′)знак равно(1v1)(Икст).{\ displaystyle {\ begin {pmatrix} x ‘\\ t’ \ end {pmatrix}} = {\ begin {pmatrix} 1 & v \\ 0 & 1 \ end {pmatrix}} {\ begin {pmatrix} x \\ t \ end {pmatrix}}.}

С двойными числами отображение т′+Икс′ϵзнак равно(1+vϵ)(т+Иксϵ)знак равнот+(Икс+vт)ϵ.{\ displaystyle t ^ {\ prime} + x ^ {\ prime} \ epsilon = (1 + v \ epsilon) (t + x \ epsilon) = t + (x + vt) \ epsilon.}

Другой взгляд на специальную теорию относительности как на неевклидову геометрию был предложен Э.Б. Уилсоном и Гилбертом Льюисом в Трудах Американской академии искусств и наук в 1912 году. Они переработали аналитическую геометрию, заложенную в алгебре расщепленных комплексных чисел, в синтетическую геометрию предпосылок. и отчисления.

Внешняя ссылка

История науки
Хронология	Алгебра  · Астрономия ( Звездная  · Солнечная система )  · Биология  · Ботаника  · Химия  · Энтомология  · Информатика  · Оптика  · Орнитология  · Патология растений  · Место женщины в науке  · Здоровье и медицина  · Методы
Науки и техники цивилизации	Египет  · Греция  · Рим  · Китай  · Индия  · Византия  · Арабский мир  · Средние века  · Османская империя  · Европейское Просвещение
Рассказы о дисциплинах	Анатомия  · Антропология  · Археология  · Астрономия ( Гравитация )  · Биология ( Морская биология  · Молекулярная биология )  · Ботаника  · Химия ( Электрохимия  · Элементы )  · Криптология  · Экология  · Экономика  · Электрофизиология  · Генетика  · География  · Геология  · Естествознание  · Ихтиология  · ИТ  · искусственный интеллект  · Лингвистика  · Логика  · Математика ( Алгебра  · Анализ  · Функциональный анализ  · Геометрия  · Вероятность  · Статистика )  · Медицина ( Хирургия  · Стоматология  · Ветеринария  · Авиационная медицина  · Медицина труда  · Неврология  · Психиатрия )  · Метеорология  · научный метод  · Минералогия  · Палеоантропология  · Палеонтология  · Психология  · Физика ( Электричество  · Механика  · Квантовая механика  · Магнетизм  · Оптика  · Общая теория относительности  · Специальная теория относительности )  · Психология ( когнитивная психология  · аналитическая психология  · Психоанализ )  · Техники  · Вулканология  · ( приматология )

• Портал истории науки
• Научный портал
• Портал истории
• Геометрический портал

Псевдо-Евклид

Евклиду приписываются два важных трактата об античной теории музыки: «Гармоническое введение» («Гармоника») и «Деление канона» (лат. Sectio canonis). Традиция приписывать «Деление канона» Евклиду идёт ещё от Порфирия. В старинных рукописях «Гармоники» авторство приписывается Евклиду, некоему Клеониду, а также александрийскому математику Паппу. Генрих Мейбомrude (1555—1625) снабдил «Гармоническое введение» обстоятельными примечаниями, и вместе с «Делением канона» приписал их к трудам Евклида.

При последующем подробном анализе этих трактатов было определено, что первый написан в аристоксеновской традиции (например, в нём все полутоны считаются равными), а второй по стилю — явно пифагорейский (например, отрицается возможность деления тона ровно пополам). Стиль изложения «Гармонического введения» отличается догматизмом и непрерывностью, стиль «Деления канона» несколько схож с «Началами» Евклида, поскольку содержит теоремы и доказательства.

После критической публикации «Гармоники» знаменитым немецким филологом Карлом Яном (1836—1899) этот трактат стали повсеместно приписывать Клеониду и датировать II в. н.э. В русском переводе (с комментариями) его впервые издал Г. А. Иванов (Москве, 1894). «Деление канона» ныне одна часть исследователей считает аутентичным сочинением Евклида, а другая — анонимным сочинением в традициях Евклида. Последние по времени русские переводы «Деления канона» опубликованы (в версии Порфирия) В.Г.Цыпиным и (в версии Боэция) С.Н.Лебедевым. Критическое издание оригинального текста «Деления канона» выполнил в 1991 г. А.Барбера.

• Назад

• Вперёд

Добавить комментарий

Четырехугольники

Про четырехугольники мы много говорим на уроках в школе: прямоугольник, квадрат, ромб.

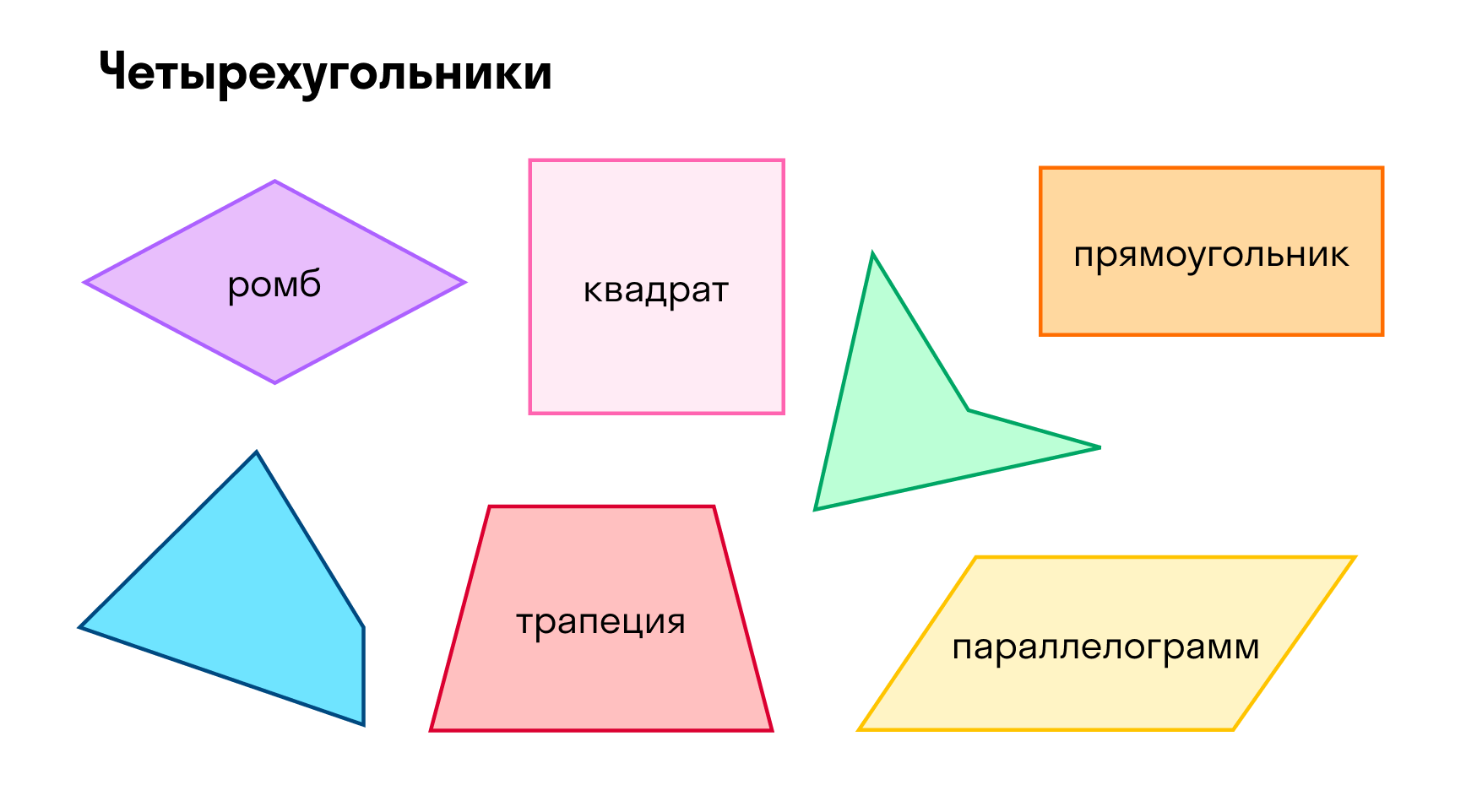
Но говорим о них не в общем случае, как для треугольников (такие вещи, как теорема синусов, косинусов), а можем формулировать только какие-то свойства для определенных видов четырехугольников.

Четырехугольникам лучше уделить побольше времени — у каждого из них есть особые свойства, которые не пригодятся для других фигур. Поэтому каждый четырехугольник лучше внимательно изучить на уроке или почитать в наших материалах:

• площадь фигуры
• периметр фигуры
• площадь прямоугольника
• периметр прямоугольника
• площадь квадрата
• периметр квадрата
• параллелограмм
• прямоугольный параллелепипед.

Геометрия всё больше приобретает роль метода мышления, метода осмысления и организации математической информации буквально во всех областях её приложения.

Подтверждение правильности сделанных мною выводов нашло в результатах опроса студентов первого курса, из которых 89% считают, что определяющим в истории геометрических знаний является личность ученого-геометра (Приложение № 3); наиболее близким к восприятию их математических знаний считается высказывание Р.Декарта «Я мыслю, следовательно, я существую» – 38% (Приложение № 4).

Значение данной работы они увидели в том, что она дает возможность: изучить методы исследований – 10%; расширить кругозор – 25%; познакомиться с основными положениями научных теорий ученых-геометров – 30%; исследовать роль личности в развитии геометрических знаний – 35% (Приложение № 5).

Таким образом, я убедилась, что исследовательская работа «История геометрии в лицах» позволила большинству студентов открыть для себя полный загадок мир геометрических знаний, поразиться многогранности таланта ученых-математиков, их любознательности, целеустремленности, трудолюбию, эрудиции.

Завершить исследовательскую работу я хочу стихами:

Как придорожные столбы

Так освещают жизни путь

Ума великие творенья.
Евклид и Фалес, и Декарт, и Ньютон,

Упорно решая науки сомненье,

Как вывод оставили мысль нам о том:

«Нет царской дороги в её изученье!»

Оно источник вдохновенья,

А Лобачевский в нем нашел

Систему взглядов геометра.

«Я мыслю – значит, существую,

Труды ученых изучая,

Их путь исканий развиваю!»

на исследовательскую работу

«История геометрии в лицах»

При изучении материалов исследовательской работы «История геометрии в лицах», я узнала много нового о жизни и достижениях великих ученых-геометров. Мне было интересно познавать новое, так как это наша жизнь, наше прошлое, наша история. А мы должны знать, что происходит в нашем мире!

Вымысел

Неевклидова геометрия часто появляется в произведениях научной фантастики и фэнтези .

• В 1895 году Герберт Уэллс опубликовал рассказ «Замечательная история глаз Дэвидсона» . Чтобы оценить эту историю, нужно знать, как идентифицируются противоположные точки на сфере в модели эллиптической плоскости. По сюжету посреди грозы Сидни Дэвидсон видит «Волны и удивительно аккуратную шхуну», работая в электротехнической лаборатории в Техническом колледже Харлоу. В конце истории Дэвидсон оказывается свидетелем HMS Fulmar у острова Антиподы .
• Неевклидова геометрия иногда связана с влиянием писателя ужасов ХХ века Л. П. Лавкрафта . В его работах многие неестественные вещи следуют своим собственным уникальным законам геометрии: в « Мифах о Ктулху» Лавкрафта затонувший город Р’льех характеризуется неевклидовой геометрией. В значительной степени подразумевается, что это достигается как побочный эффект несоблюдения естественных законов этой вселенной, а не просто использования альтернативной геометрической модели, поскольку ее явная врожденная неправильность, как говорят, способна свести с ума тех, кто смотрит на нее.
• Главный герой романа Роберта Пирсига « Дзен и искусство ухода за мотоциклами» неоднократно упоминал риманову геометрию.
• В «Братьях Карамазовых» Достоевский обсуждает неевклидову геометрию через своего персонажа Ивана.
• Роман Кристофера Приста « Перевернутый мир» описывает борьбу жизни на планете с формой вращающейся псевдосферы .
• Роберт Хайнлайн в своей книге « Число зверя» использует неевклидову геометрию для объяснения мгновенного переноса в пространстве и времени, а также между параллельными и вымышленными вселенными.
• HyperRogue от Zeno Rogue — это игра в жанре roguelike, действие которой разворачивается на гиперболической плоскости , позволяя игроку испытать многие свойства этой геометрии. Многие механики, квесты и локации сильно зависят от особенностей гиперболической геометрии.
• В Renegade Legion научной фантастики настройки для ФАЗА «s Wargame , ролевые игры-игры и вымысла, быстрее чем свет путешествия и связи возможно за счет использования Се Хо Polydimensional неевклидовой геометрии, опубликованной когда — то в середине 22 век.
• В Флаттерленде» Яна Стюарта главный герой Виктория Лайн посещает самые разные неевклидовы миры.

«Начала» Евклида

Главный труд Евклида – «Начала» (или «Элементы», в оригинале «Стойхейа»). «Начала» Евклида состоят из 13 книг. Позднее к ним были прибавлены еще две книги.

Первые шесть книг «Начал» посвящены геометрии на плоскости – планиметрии. В философско-теоретическом отношении, в плане философии математики особенно интересна первая книга, которая начинается с определений, постулатов и аксиом, учение о которых было заложено Аристотелем.

Евклид определяет точку как то, что не имеет частей. Линия – длина без ширины. Концы линии – точки. Прямая линия равно расположена по отношению к точкам на ней. Поверхность есть то, что имеет только длину и ширину. Концы поверхности – линии. Плоская поверхность есть та, которая равно расположена по отношению к прямым на ней. И так далее. Таковы определения Евклида.

Статуя Евклида в музее Оксфордского университета

Далее следуют постулаты, т. е. то, что допускается. Допустим, что от всякой точки до всякой точки можно провести прямую линию, что ограниченную прямую можно непрерывно продолжить по прямой, что из любой точки, принятой за центр, можно всяким раствором циркуля описать круг, что все прямые углы равны между собой и что если прямая, падающая на две прямые, образует внутренние и по одну сторону углы, меньшие двух прямых, то, будучи продолженными, эти две прямые рано или поздно встретятся с той стороны, где углы меньше двух прямых.

Аксиомы Евклида говорят о том, что величины, равные третьей величине, равны между собой, что если к равным прибавить равные, то и целые будут равными, и т. д.

Далее, в первой же книге «Начал» Евклида, рассматриваются треугольники, параллельные линии, параллелограммы. Вторая книга «Начал» содержит геометрическую алгебру: числа и отношения чисел выражаются в пространственных величинах и в их пространственных же отношениях. Третья книга «Начал» исследует геометрию круга и окружности, четвертая – многоугольники. Пятая книга дает теорию пропорций как для соизмеримых, так и для несоизмеримых величин. В книге VI Евклид прилагает эти теории к планиметрии. Книги VII – X содержат теорию чисел, причем X книга трактует иррациональные линии. XI, XII и XIII книги «Начал» посвящены стереометрии, при этом в XII книге применяется метод исчерпания.

В строгом смысле слова Евклида нельзя считать «отцом геометрии». Свои «Начала» были у Гиппократа Хиосского в V в. до н. э. В IV в. до н. э. «Начала» были у Леона, и у Феудия Магнесийского. Метод исчерпания применял Евдокс Книдский, возможный учитель Евклида по Академии. Проблемой иррациональности занимались пифагореец Гиппас Метапонтский, Феодор Киренский, Теэтет Афинский… Однако Евклид – не простой передатчик сделанного до него математиками. В «Началах» Евклида мы видим завершение математики как стройной науки, исходящей из определений, постулатов и аксиом и построенной дедуктивно. Математика Евклида – вершина древнегреческой дедуктивной науки. Она резко отличается от ближневосточной математики с ее практической приблизительной рецептурностью. Не случайно «Начала» Евклида по их логической стройности, ясности, изяществу и законченности сравнивают с .

Правда, существовала легенда, что сам Евклид – не единственный автор дошедших до нас «Начал», что он сам дал лишь догматическое изложение материала, без доказательств, что доказательства были добавлены вышеупомянутым Теоном Александрийским. Теон Александрийский действительно занимался проблематикой «Начал». Но не он один. Этим же занимались и Прокл, и Симплиций. «Начала» Евклида были частично переведены на латинский язык Цензорином и Боэцием. Но эти их переводы затерялись. На Западе вплоть до конца XII в. находились в обращении тезисы Евклида без доказательств.

Что касается Ближнего Востока, то там Евклид был известен в переводах с греческого на сирийский, а с сирийского – на арабский. Первым арабским философом, который заинтересовался Евклидом, был, по-видимому, аль-Кинди (IX в.). Его интерес ограничивался евклидовой «Оптикой». Однако затем последовала масса переводов и комментариев на «Начала». Эти арабские тексты были переведены в XIII в. на латинский язык. Первый латинский перевод с греческого оригинала был делан в Европе в 1493 г. и отпечатан в 1505 г. в Венеции. Но до 1572 г., когда Федерико Коммандино в своем латинском переводе исправил эту ошибку, Евклида-математика путали с Евклидом Мегариком.